Contexte & description du projet
Chronologiquement le premier projet exposé sur ce site (entre octobre et décembre 2024, honnêtement je ne sais plus quel mois), celui-ci correspond à la Situation d'Apprentissage et d'Évaluation (SAE) "Comparaison d'approches algorithmiques". L'objectif est de se familiariser seul avec des techniques de base de test de satisfiabilité booléenne via l'implémentation d'un solveur SAT et d'utiliser la résolution SAT pour résoudre des Sudoku.
Méthodologie et outils
Le projet se présentait sous la forme d'un ensemble de fonctions Python à implémenter, avec pour seules informations des spécifications in/out et des tests unitaires incomplets. Pour chaque fonction, il y avait donc une phase de compréhension des besoins, puis d'implémentation et enfin de test. J'ai implémenté les fonctions sur l'IDE Visual Studio Code.
Plusieurs solutions étaient envisageables pour le solveur SAT, on est donc parti sur une approche de backtracking simple puis on a ajouté des optimisations au fur et à mesure vers du DPLL. La plupart des fonctions étant réutilisées pour les suivantes, il fallait être sûr du bon fonctionnement de chacune avant de passer à la suivante.
Contributions personnelles
Ce projet étant individuel, toutes les parties ont été réalisées par mes soins.
Résolution de problème SAT
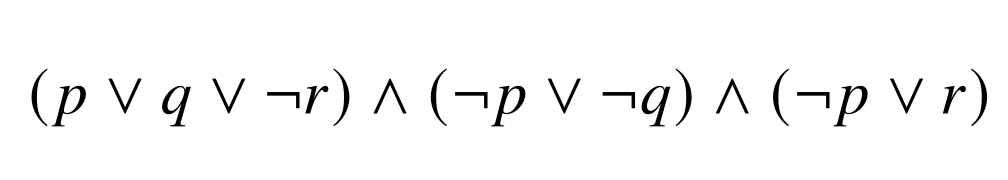
Exemple de formule SAT en CNF : réaliser les conditions (p ou q ou non-r) ET (non-p ou non-q) ET (non-p ou r)
Prenons comme entrée une formule booléenne exprimée en forme normale conjonctive (CNF), c'est-à-dire une conjonction de clauses, où chaque clause est une disjonction de littéraux. On représentera cela par une liste (formule) de listes (clauses) de booléens (littéraux). L'objectif est de déterminer si une formule est satisfiable ou non et, si oui, renvoyer une valuation (c'est-à-dire donner une valeur à chaque littéral) permettant de vérifier la formule.
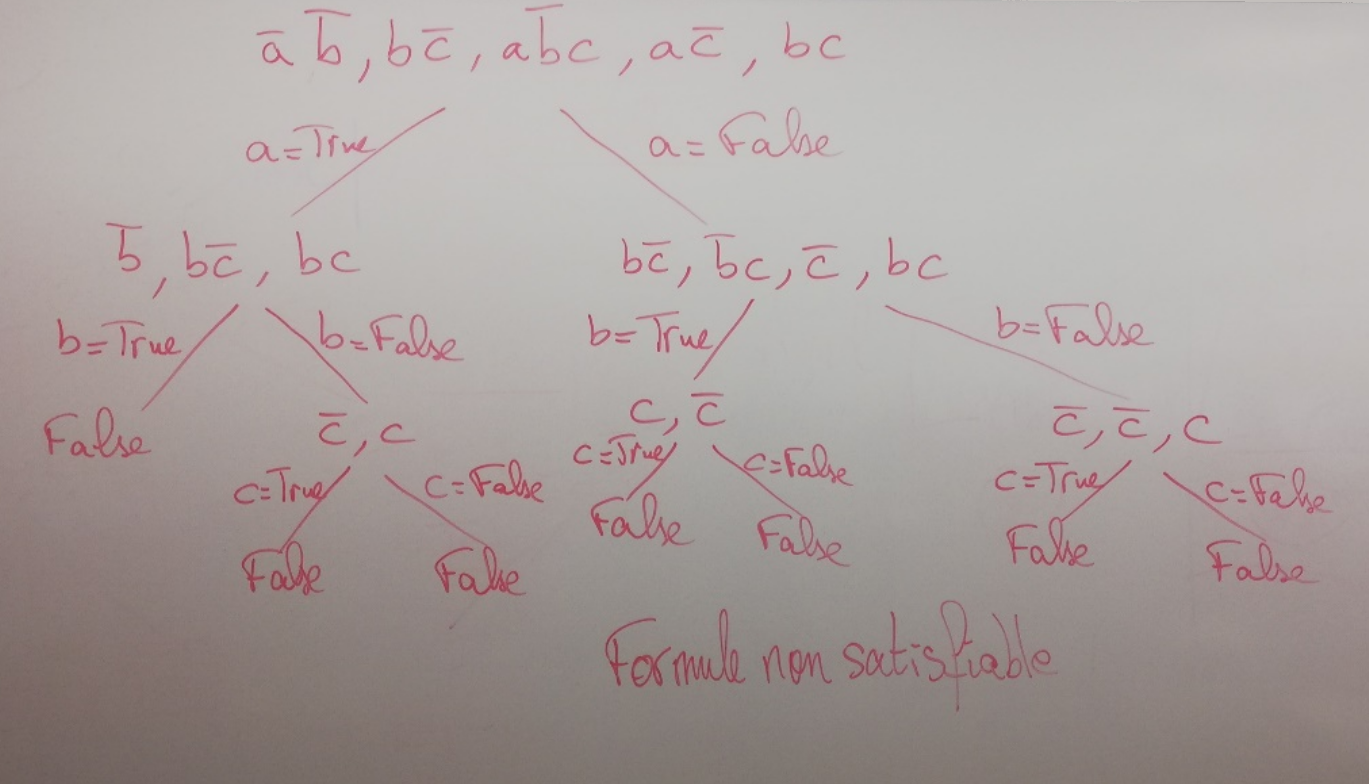
Exemple de parcours d'arbre pour le backtracking
Pour cela, j'ai commencé par étudier la satisfiabilité d'une clause à partir d'une valuation arbitraire puis j'ai étendu cela à la formule entière. Par la suite, j'ai implémenté une méthode simple de backtracking pour parcourir l'"arbre" des valuations possibles (par récursivité) et tester à chaque fois la satisfiabilité de la formule avec la valuation courante. La solution apportée est déjà fonctionnelle, mais je pouvais l'optimiser : d'une part, en simplifiant la formule à vérifier pour gagner du temps dans la vérification de la satisfiabilité. D'autre part, en passant sur une solution DPLL pour simplifier encore la résolution (en retirant les clauses unitaires et les littéraux purs).
Modélisation d'une grille de Sudoku
Le point principal de cette partie est de traduire les règles d'un sudoku en une formule en CNF afin de pouvoir utiliser le solveur SAT développé précédemment pour résoudre la grille. J'ai aussi pris en compte les chiffres déjà présents dans la grille afin de débuter avec une valuation partielle et une formule simplifiée (grâce aux fonctions de simplification).
Résultats et livrables
Au bout du compte, mes réalisations ont correctement répondu aux attentes, étant donné le succès des tests, à l'exception de deux fonctions : si mon travail a permis de faire fonctionner un solveur SAT par backtracking simple en Python, ainsi que sa première version simplifiée, la fonction de parcours récursif de l'arbre en DPLL n'a pas été réussie, bien que les méthodes de progression et de retour dans l'arbre avec DPLL passent leurs tests respectifs. Quant à la modélisation du Sudoku, il me manque les clauses vérifiant la contrainte "pas plus d'une fois le même chiffre par région", ce qui me laisse à 334 clauses sur les 368 attendues pour un Sudoku 4x4. Malgré tout, j'ai été noté 19.20/20.
L'unique livrable attendu est le code Python complet du solveur SAT et de la modélisation du Sudoku, accompagné des tests unitaires fournis. Vous pouvez librement le consulter en cliquant ici.
Compétences développées
Ce projet m'a surtout permis d'améliorer ma capacité à modéliser des problèmes (énoncés) sous une forme logique et algorithmique, ce qui m'aura été très utile pour le projet Quadtree notamment. Par ailleurs, le temps accordé en cours pour ce projet a été faible, une notion d'organisation et d'autonomie pour le travailler en dehors des horaires de cours a donc été nécessaire.
Bilan
Ce projet, bien que frustrant par certains aspects (honnêtement cela m'ennuie de présenter un projet imparfait), m'aura permis de me familiariser avec la résolution de problèmes logiques et la programmation récursive. J'ai beaucoup aimé analyser les spécifications et réfléchir à un moyen de les implémenter. Si le projet était à refaire, je passerai plus de temps à tester chaque fonction pour m'assurer de leur bon fonctionnement avant de les intégrer dans un système plus complexe.