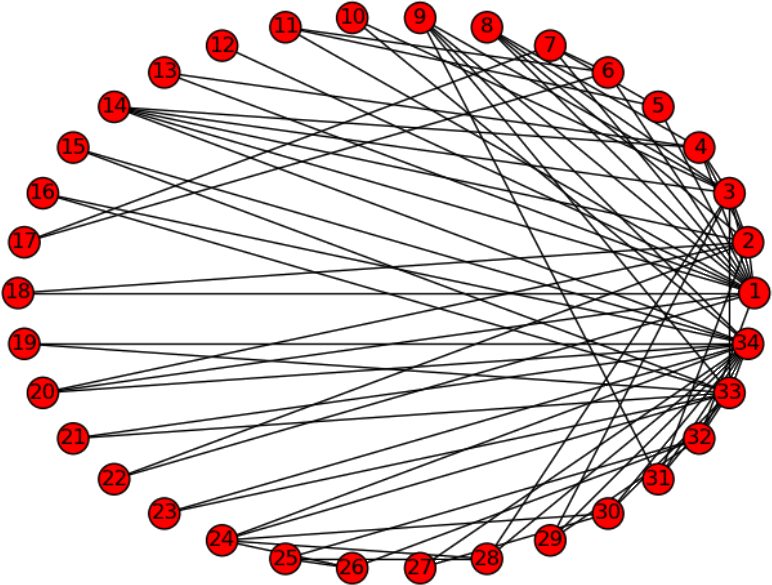
Contexte & description du projet
Ce projet intervient en avril 2025, dans le cadre de la Situation d'Apprentissage et d'Évaluation (SAE) "Exploration algorithmique d'un problème". L'objectif de cette SAE sur les graphes est d'implémenter des algorithmes de calcul de plus courts chemins et d'utiliser ceux-ci pour faire une initiation à l'analyse de réseaux sociaux, réseaux à convertir entre le langage Python et des fichiers .dot. Le projet était à réaliser par groupes de 2.
Méthodologie et outils
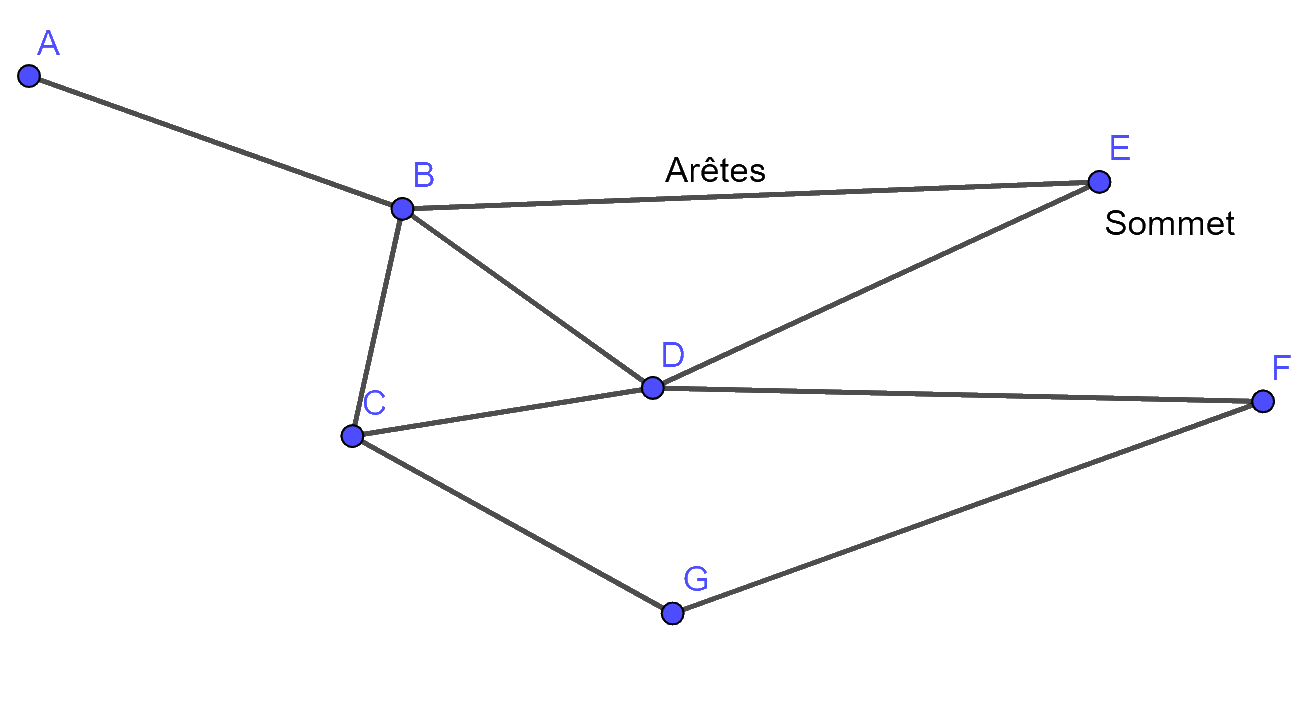
Principe d'un graphe : les sommets sont reliés entre-eux par des arêtes
Le principe est de compléter un ensemble de méthodes en Python à partir de recherches sur Internet, de documents et/ou de nos connaissances sur le cours. L'ordre logique pour réaliser le projet était de commencer par les fonctions de la classe représentant les graphes (calcul de degrés, connexité, chemins, etc.), puis les algorithmes de recherche de plus court chemin (Dijkstra, Bellman-Ford, Floyd-Warshall), et enfin l'analyse de réseaux sociaux avec leurs métriques. Chaque fonction a été testée et les algorithmes comparés entre eux sur plusieurs graphes. J'ai travaillé sur l'IDE Visual Studio Code.
Contributions personnelles
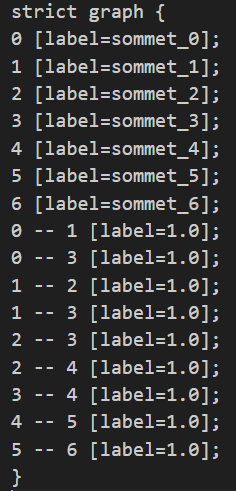
Exemple d'un fichier .dot
Méthodes des graphes
Cette première partie était très courte, avec mon collègue on a écrit une fonction sur deux chacun. Je ne saurais pas me rappeler qui a fait quoi précisément, étant donné la vitesse à laquelle nous avons avancé (pas eu le temps de me marquer), cependant le résultat comprenait le calcul de : nombre de sommets / d'arêtes, degré d'un sommet / des sommets (liste), successeurs et descendants d'un sommet, connexité et plus grande composante connexe, arc et chemin, valeur d'un chemin, nature orientée ou non du graphe et une transition de graphe orienté vers non-orienté. Je me suis aussi occupé de la création de graphe à partir de fichier .dot suivant un formatage précis. Les méthodes ont été documentées et testées.
Algorithmes de recherche de plus court chemin
Trois classes étaient à construire, sur la base d'une classe-mère, chacune implémentant un algorithme différent : Dijkstra, Bellman-Ford et Floyd-Warshall. Ces algorithmes permettent de calculer les plus courts chemins dans un graphe pondéré, avec des contraintes et des performances différentes. Bien que je ne me rappelle plus qui a fait Djikstra, je me souviens avoir implémenté Floyd-Warshall pendant que mon collègue s'occupait de Bellman-Ford. Nous avons comparé leur efficacité et leur applicabilité sur 3 graphes dont un très grand (200 sommets, 350 arêtes) pour apercevoir des différences plus claires. J'ai aussi réalisé une fonction pour générer une matrice et la sauvegarder dans un fichier .dot à partir du nombre de sommets, le nombre d'arêtes et le nom du fichier souhaités.
Analyse de réseaux sociaux
Dans cette dernière partie, il suffisait d'implémenter des méthodes pour calculer les métriques d'un réseau social. Bien que je ne sache plus non plus ce que j'ai fais parmi le degré moyen du graphe, la proximité d'un sommet, le diamètre du graphe et sa longueur moyenne (probablement la moitié), je me rappelle très clairement avoir appliqué ces métriques sur des réseaux contenus dans des fichiers .dot et rédigé dans le rapport les résultats observés. Les métriques ont été testées en calculant avec papier/crayon les résultats attendus.
Résultats et livrables
Le résultat de ce projet résulte en des classes fonctionnelles pour l'analyse de graphes et de réseaux. La comparaison des algorithmes a permis de mieux comprendre leurs avantages et inconvénients respectifs (Djikstra, par exemple, est de loin le plus rapide, mais ne supporte pas les arcs avec poids négatif). Pour ce projet, j'ai été gratifié de la note de 16/20 (la meilleure note de la promotion fut 18).
2 imperfections dans notre travail sont à relever : notre algorithme de Djikstra ne prévoit pas d'assertion en cas d'arc de valeur négative, et mon algorithme de Floyd-Warshall utilise une boucle de trop, multipliant le temps d'exécution par n-2 (où n est le nombre de sommets du graphe) et renvoyant un résultat légèrement erroné.
Ont été rendus le code source complet, les fichiers .dot utilisés et générés, ainsi qu'un rapport au format markdown détaillant la comparaison des algorithmes de calcul de plus court chemin ainsi que les résultats des métriques d'analyse de réseaux sociaux. En anonymisant mon collègue, je peux vous proposer l'intégralité des livrables ici.
Compétences développées
Ce projet m'a permis de me familiariser avec les concepts des graphes et des réseaux, ainsi que progresser en programmation Python. J'ai aussi appris à manipuler des fichiers depuis le langage Python aussi bien en lecture qu'en écriture, ce qui est une compétence utile pour exporter des données et les représenter sous plusieurs formes (connaissance réutilisée et améliorée dans le projet PortfoLaurens). Enfin, travailler en binôme m'a également aidé à améliorer mes compétences en communication et collaboration, essentielles dans toute équipe informatique.
Bilan
En conclusion, ce projet a été une excellente occasion de découvrir les algorithmes de graphes et réseaux (sujets que j'aime beaucoup, soit dit en passant) et une première expérience dans la gestion de fichiers depuis Python. Le projet dans sa globalité est un peu léger mais il n'en reste pas moins que je l'ai apprécié.